Cuerpos redondos y de revolución

 Sólido de revolución

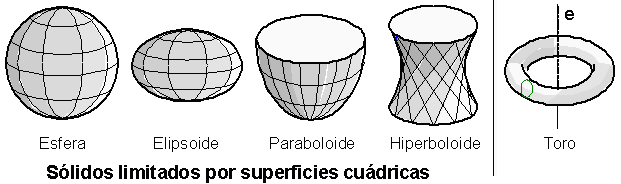
Cuerpo redondo limitado por una generatriz (g) curva, que rota alrededor de un eje (e). Entre ellos se pueden mencionar:

• sólidos limitdos por superficies cuadricas:
  • esfera: la generatriz es una circunferencia,
  • elipsoide: la generatriz es una elipse,
  • paraboloide: la generatriz es una parábola,
  • hiperboloide: la generatriz es una hipérbola,
• toro (anillo). Su superficie la genera una circunferencia ó una elipse, que gira alrededor de un eje (e), coplanar con ella, y situado fuera de ella.

 

Cilindro

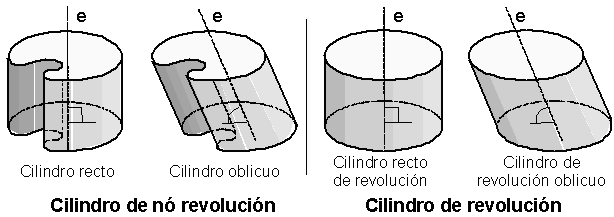
Cuerpo redondo limitado por una superficie cilíndrica y dos bases planas paralelas. La recta que pasa por los centros geométricos de las bases se denomina eje del cilindro (e), y es paralela a la generatriz (g) de la superficie cilíndrica. Los cilindros pueden ser:

• cilindro recto: si el eje (e), es perpendicular a las bases,
• cilindro oblicuo: si el eje (e), no es perpendicular a las bases,
• cilindro de revolución: si está limitado por una superficie cilíndrica de revolución. Pueden a su vez ser:
  
  
  • cilindro de revolución recto: si el eje (e), es perpendicular a las bases,
  • cilindro de revolución oblicuo: si el eje (e), no es perpendicular a las bases.
   
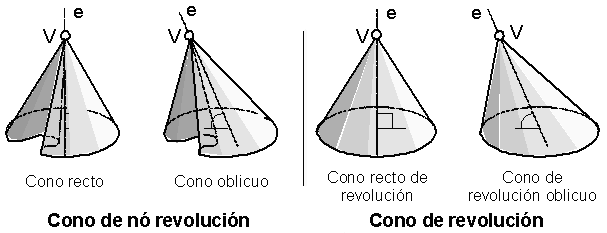
• Cono
  Cuerpo redondo limitado por una superficie cónica y por una base plana. La recta que pasa por el vértice (V), de la superficie cónica y el centro geométrico de la base se denomina eje del cono (e). Los conos pueden ser:
• cono recto: si el eje (e), es perpendicular a la base,
• cono oblicuo: si el eje (e), no es perpendicular a la base,
• cono de revolución: si está limitado por una superficie cónica de revolución. Pueden a su vez ser:
  • cono de revolución recto: si el eje (e), es perpendicular a la base,
  • cono de revolución oblicuo: si el eje (e), no es perpendicular a la base.